Kriging en Cuerpos: ejemplo de cálculo de la ley de un bloque
Breve Explicación Teórico / Práctica:
Si visualizamos una veta con tajeos delimitados por galerías y chimeneas como indica la figura 1, podemos extraer un tajeo y mostrarlo como indica la figura 2, en donde se observan las dimensiones del tajeo, las leyes y la potencia (asumiremos que las chimeneas tienen sus leyes y potencias definidas).Una matriz de bloques (a 3D) que encierra a un cuerpo mineralizado, es conocido como "Modelo de Bloques" , normalmente este modelo esta cortado por la superficie topográfica, perforado por taladros con muestras de leyes de interés. Si realizamos, en cierta sección vertical, la extracción de una tajada de bloques de esa matriz y mostramos los taladros cercanos a esa sección observamos la Fig. Nº 1.
Las leyes de los taladros, normalmente deben tener una longitud regular (igual), se acostumbró compositarlos a una longitud igual a la altura del banco de operaciones del tajo. Sin embargo considero que el cálculo de compositos debe orientarse a mantener una igualdad en la longitud de todas las muestras, y no necesariamente a la longitud del banco de operaciones.
Con esta información regular se procede al cálculo del variograma, en lo posible, en todas las direcciones de una esfera, buscando las mas representativas y que guarden relación con las ocurrencias de campo y las interpretaciones de los geólogos con experiencia en el terreno.
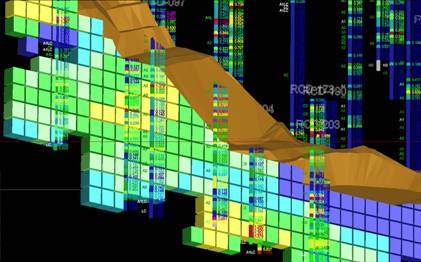
Fig. 1: Sección de Bloques con taladros
La variografía, es uno de los instrumentos mas importantes e la Geoestadística, por ello es recomendable realizar cálculos de variogramas en todas las direcciones posibles del depósito.
Por lo general el cálculo parte en la dirección de azimuth cero, para este azimuth se debe calcular los variogramas para los buzamientos que van desde 80º hasta -90º variando la dirección de cálculo cada 15º.
Habiendo culminado los cálculos para este azimuth cero, se cambia la dirección a 15º de azimuth y se calculan los variogramas para los mismo buzamientos. Así sucesivamente se varía la dirección del azimuth desde 00º hasta 165º.
Estas direcciones deberán ser tomadas como sugerencia, el mismo que podrá variar de acuerdo a las características del depósito y de acuerdo al número de muestras disponibles.
En base a los resultados del variograma, se determinarán los radios de influencia en las direcciones preferenciales así como las anisotropías de correlación entre las muestras.
Para la construcción del elipsoide de la figura 3, se encontraron variogramas experimentales (figura 2) con alcances distintos en direcciones perpendiculares entre ellas. Esto indica la presencia de anisotropía que es muy común en casi todos los depósitos.
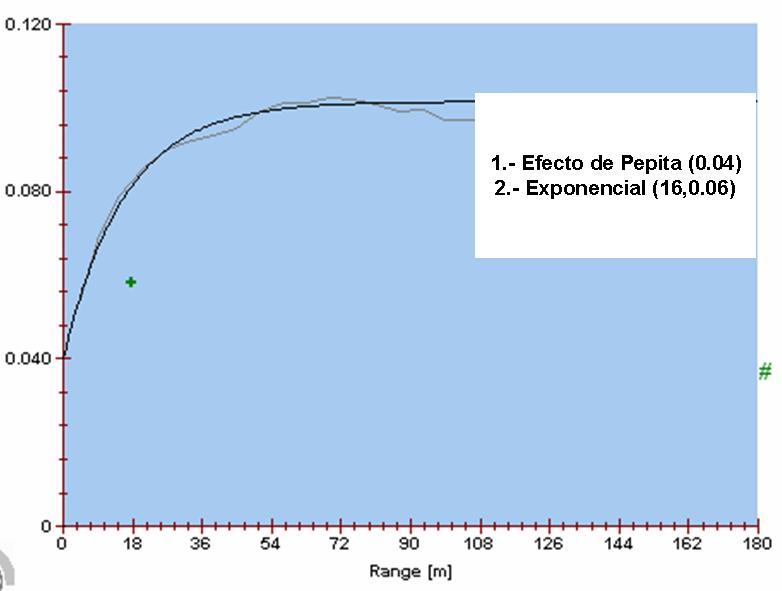
Fig. 2: Variograma Experimental y Modelo de Variograma
Para determinar el modelo del variograma, se debe calcular el variograma experimental, que debe ser determinado en todas las direcciones posibles del depósito.
En el gráfico adjunto, se muestra el variograma experimental con el modelo de variograma exponencial siguiente:
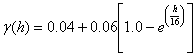
Cada punto del variogram experimental es la medida de la discrepancia promedio entre leyes distanciada a "h" metros (en el gráfico el eje horizontal Range).
En cierta forma, el variograma, es un indicador de como se incrementan las discrepancias entre las muestras a medida que se van distanciando entre si. ó cuando el valor de "h" crece.
El modelo matemático que se ajusta al variograma experimental se aplicará en el krigeage.
Luego de encontrar la dirección preferencial de mineralización mediante los variogramas experimentales, se aplica la modelización (figura 2) con las fórmulas autorizadas como: esférico, exponencial, lineal, gausiano, etc. En forma similar se debe aplicar la modelización en las direcciones perpendiculares a la dirección preferencial.
Este análisis permitirá encontrar las anisotropias en la mineralización del depósito y determinar los radios de influencia de las leyes en las direcciones principales.
Para la estimación de la ley de un bloque, es necesario que las muestras se encuentren "regularizadas", es decir que mantengan la misma longitud, esto se logra con los procedimientos de "cálculo de compósitos" que encuentra los valores de leyes en muestras de igual longitur.
Con las muestras regularizadas, se coloca al centro del elipsoide cada uno de los elementos del Modelo de Bloques, de tal forma que la estimación se realice individualmente para cada uno, tomando como dato de cálculo toda información que se encuentren al interior del elipsoide.
Para mejor explicación del cálculo de la ley de un bloque, se tomará la figura 3, en donde asumiremos que el elipsoide presenta una radio mayor de 30 metros y radios menores perpendiculares de 15 metros. Con estos distancias, del conjunto de muestras de los taladros hemos seleccionado 4 muestras que caen al interior del elipsoide.
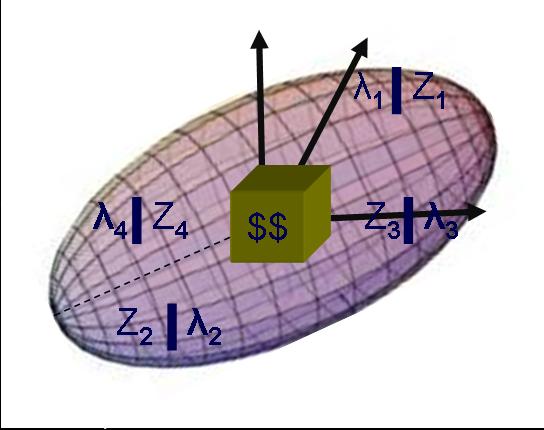
Fig. 3: Elipsoide de influencia, con block a estimar
Este elipsoide se utilizará para cada bloque a estimar, es decir navegará por todo el modelo de bloques construido para el depósito.Las coordenadas centrales del elipsoide y del bloque deberán se coincidentes.
Las muestras se ubican en 3D según las coordenadas de su punto medio. Los valores de las leyes de las muestras se representan porz(i). Para este ejemplo, tenemos 4 muestras y un volumen a estimar de 10x10x10 m3.
Para propósitos de cálculo se entenderá que el bloque esta representado por una malla de puntos en su interior de 4x4x4 puntos.
Al utilizar cuatro muestras, se asignará a cada una un peso "lamda" ( ?), este peso depende de la distancia de la muestra al bloque, o también depende si existen algunas otras muestras intermedias que ocasionan apantallamiento. El objetivo del krigeage es determinar los valores de los ( ?), una vez conocido recién se podrá calcular la ley del bloque mediante la expresión de la figura Nº 4.
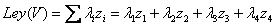
Fig. 4: Ley del bloque (V) a estimar
Conocido los valores de los pesos el cálculo de la ley estimada se obtiene como indica la fórmula de la fig. 5.
Para determinar el peso de cada muestra se aplicará, para esta explicación, el krigeage ordinario, su aplicación requiere conocer el significado de cada una de las variables de la siguiente formulación matemática que se aplicará:
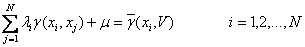
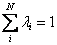
Fig. 6: Sistema de Ecuaciones Krigeage
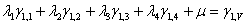
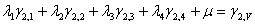
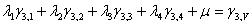
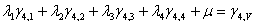
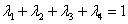
Fig. 7: Sistema de Ecuaciones de Krigeage (expandido)
En donde los símbolos "lamda" ( ?) son los pesos para cada ley (j), los "gama i j " son el promedio de aplicar el variograma entre las geometrías (i) y (j) que corresponden a cada una de las galerías, chimeneas y tajeo, como se explica a continuación:
Con la fórmula del modelo del variograma (figura 3) y la indicación gráfica de la Fig. 4, entre el punto (1) y el mismo punto (1) se calcula el gama(1,1).
Luego se calcular el gama(1,2), que es el valor del gama(h) entre los puntos (1) y (2), de la misma forma se continúa con gama(1,3),..., y gama(4,4).
A continuación se calcula el gama(1,v), gama (2,v),..., hasta el gama (4,v). Tambien se calcula el gama (v,v).
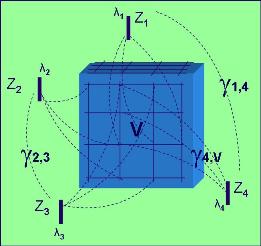
Fig. 8: Descripción Geométrica de forma de cálculo de los gama(i,j)
Con la fórmula del modelo del variograma (figura 4) y la indicación gráfica de la Fig. 6, se calcula el gama(1,1) entre los puntos de la galería (1) y los mismos puntos de esta galería (1).
Luego se calcular el gama(1,2), que es el promedio del variograma entre los puntos de la galería (1) y la galería (2), de la misma forma se continúa con gama(1,3),..., y gama(4,4).
A continuación se calcula el gama(1,V), gama (2,V),..., hasta el gama (4,V). Tambien se calcula el gama (V,V).
Este texto es para quienes desean mayor explicación sobre el cálculo de los gama(i,j)
Por ejemplo para el cálculo del gama(2,3), se tomará el punto (2) y el otro extremo de "h" se ubicará en el punto (3), se calcula la distancia absoluta (por diferencia de coordenadas) y esta distancia se reemplaza en la fórmula del modelo del variograma (figura 2), se calcula el valor que da la fórmula y se registra como un primer valor. Se debe entender que este valor es igual a gama(3,2).A continuación se vuelve a tomar el punto (2), y en el otro extremo de "h" se ubica el punto (3), se calcula la distancia entre estos dos nuevos puntos, esta distancia al reemplazar en la fórmula de la figura 2, originará otro valor que se debe sumar al anterior resultado.
Luego se sigue la misma forma de cálculo, para todas las posibles interacciones entre la 4 muestras, hasta completar de calcular todos los gama(i,j).
Para el cálculo de los gama(i,v), es decir gama(1,v), gama(2,v)......, gama(4,v), se considerará que el bloque "v" esta conformado por puntos en su interior con una distribución interna de 4 puntos en el eje x, 4 puntos en el eje y, cuatro puntos en el eje z, totalizando en su interior 64 puntos.
Esto significa que para calcular el gama(1,v), el punto (1) tendrá que interactuar con los 64 puntos que representa al volumen.
Hasta aquí hemos terminado los cálculos de los gama(i,j) y gama(i,V), y tenemos definido el sistema de ecuaciones de krigeage, quedando solo las incognitas "lamda" ( ?) , que se resuelven aplicando cualquiera de los procedimientos conocidos, y si estas ecuaciones son numerosa, aplicando cualquiera de las rutinas de solución de ecuaciones lineales difundidas en la web.
Antes de terminar este punto, es importante destacar que estos procedimientos de cálculo son aplicables mediante casi todos los software especializados y que cuenten con módulos de cálculos geoestadísticos, sin embargo es necesario conocer como identificar y asignar los correctos valores geoestadisticos en los menus o pantallas que guian el proceso de estimación de recursos
Reciba asesoramiento para este proceso de cálculoEn Geoestadistica.com encontrará las respuestas mas convincentes para confiar en la calidad y cantidad de sus recursos, la aplicación de la mas alta tecnología mediante los software disponibles o no en su empresa, garantizaran la verificación de los resultados.Para mayor información contáctenos. |