Diseño de Minas a Cielo Abierto: Algoritmo de Grafos de Learchs y Grossman
DEFINICIONES BÁSICAS
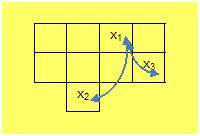 Fig. 1 |
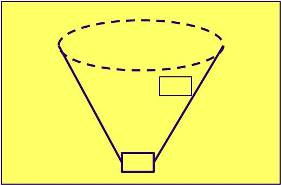 Fig. 1a |
Camino: Es una secuencia de arcos tal que el vértice final de cada uno de ellos corresponda al vértice inicial del siguiente. No interea la orientación de los arcos, Fig. 2.
Circuito: Es un camino donde el vértice inicial y final coínciden, es decir las orientaciones son en un solo sentido, Fig. 3.
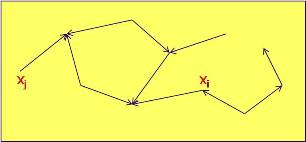 Fig. 2 |
 Fig. 3 |
Arista: Es un conjunto e(i) = (X,Y) de dos elementos que pueden ser (X,Y) pertenecientes al conjunto A de arcos, o (Y,X) también pertenecientes a A. Se diferencian del arco porque la arista no implica orientación.
Cadena: Es una secuencia de aristas (e1, e2, .... , en) donde cada arista tiene un vértice en común con el siguiente, Fig. 4.
Ciclo: Es una cadena donde los vértices inicial y final coínciden, Fig. 5.
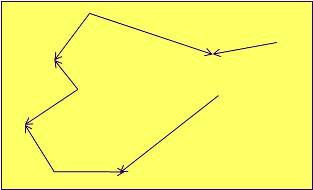 Fig. 4 |
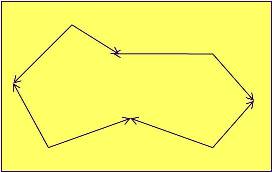 Fig. 5 |
Sub-Grafo: Se llama sub-grafo de G(X,A) al conjunto de vértices Y de X, y comprendiendo a todos los arcos que conectan los vértices de Y en G, se denota por G(Y,Ay), Fig. Nº 6a y 6b.
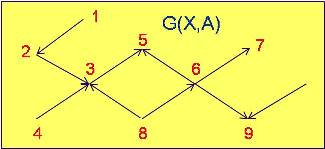 Fig. 6a |
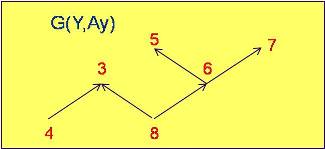 Fig. 6b |
En donde:
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {(2,1), (3,2), (4,3), (8,3), (3,5), (8,6), (6,5), (9,6), (6,7), (9,10)}
Y = {3, 4, 5, 6, 7, 8}
Ay = {(4,3), (8,3), (8,6), (6,5), (6,7)}
 Fig. 6a |
 Fig. 6b |
Grafo Parcial: El grafo parcial G(X,B) de un grafo G(X,A) es un conjunto de arcos B contenido en A y conteniendo todos los vértices de G(X,A), Fig. 7.
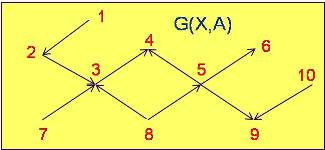 Fig. 7a |
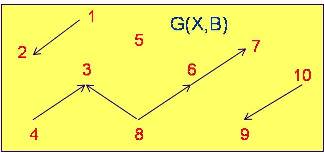 Fig. 7b |
En donde:
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {(2,1), (3,2), (3,4), (5,4), (5,6), (7,3), (8,3), (8,5), (9,5), (9,10)}
B = {(2,1), (7,3), (8,3), (8,5), (5,6), (9,10)}
Cierre de un Grafo Orientado: Se denomina cierre de un grafo orientado G(X,A) a un conjunto de vértices Y perteneciente a X que cumplen la condición.
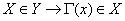
Para todo vértice X perteneciente al conjunto de vértices Y, implica que cualquier elemento perteneciente al cono (formado a partir de X) pertenezca al conjunto Y.
Sea el conjunto Y de vértices pertenecientes a un "pit". Fig. 8.
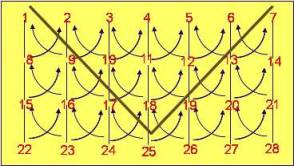
Y = {2, 3, 4, 5, 6, 10, 11, 12, 18}
Tomemos un punto x del conjunto Y. Por ejemplo el 18, vemos que x pertenece a Y, además que todos los elementos del cono (es decir los primeros vértices a minar antes de llegar a X) están contenidos en ?(x) = ?(18) = {2, 3, 4, 5, 6, 10, 11, 12, 18}
Vemos que si Y es un cierre de G(X,A), entonces G(Y,Ay) es un sub-grafo cerrado de G(X,A). Además por definición el conjunto nulo Y=0 es también un cierre de G(X,A).
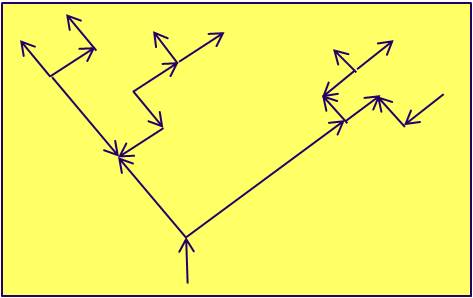
Árbol: Es un grafo orientado que no contiene ningún ciclo. Se le denomina por T=(X,C). Fig. 9:
Raíz: Cualquier vértice de un árbol puede ser raíz. Fig. 10:
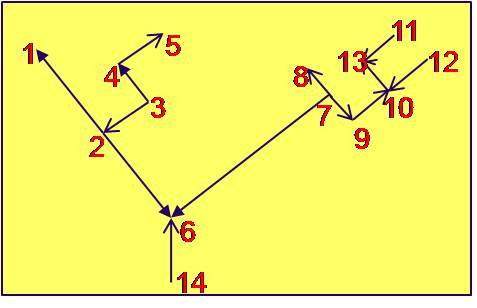 Fig. 10a |
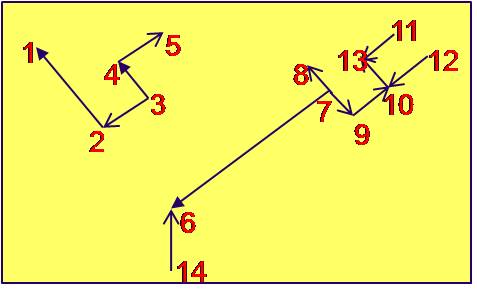 Fig. 10b |
Por ejemplo en la figura si suprimimos un arco (2,6) se obtienen 2 componentes. El componente T1 = (X1, A1) que no contiene la raíz se llama ramo de T = (X,C), la raíz del ramo es el vértice del ramo adyacente del arco (2,6). Este vértice adyacente es el 2.
Los ramos de un ramo le llamaremos "ramitos".
EL PROBLEMA
Con estas definiciones de base pasamos a anunciar el problema:Dado un conjunto de bloques v(i) de valor m(i), que encierra el yacimiento, estos bloques pueden formar un grafo orientado G(X,A), es decir cada v(i) constituye un vertice x(i) del grafo con un valor m(i), y todos los arcos A están orientados hacía la "superficie", Fig. Nº 11.
Fig. 11
Se necesita hallar el cierre G(Y,Ay) tal que la suma de las masas m(i) que lo contienen, sea máxima.
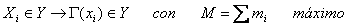
todo vértice Xi que pertenezca a Y (vértices del cierre máximo) implica que el árbol (o ramo) que forman los vértices Xi , también pertenezcan a Y, Fig. 12:
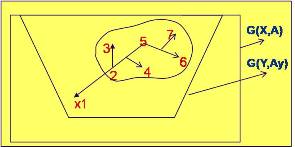
Fig. 12
Los vértices x = 1, 2, 3, 4, 5 pertenecen a Y, para que sea un cierre máximo T(X) debe pertenecer a Y.
DESARROLLO DEL ALGORITMO
El procedimiento que se explicará en pocos pasos más adelante, empieza con la construcción de un árbol To en G. Luego To es transformado en sucesivos árboles T1, T2, .... , Tn, según determinadas reglas hasta que ya no sea posible ninguna transformación. Entonces el cierre máximo viene formado por aquellas ramas conocidas del árbol final.La transformación de los sucesivos árboles Ti, pueden ser realizados teniendo en cuenta ciertas propiedades que describiremos a continuación:
- Cada arista ek (arco ak) de un árbol T, define una rama; Tk = (Kk, Ak)
- Se llamará a Xk, la raíz de la rama Tk
- La masas Mk de una rama Tk es la suma de las masas de los vértices
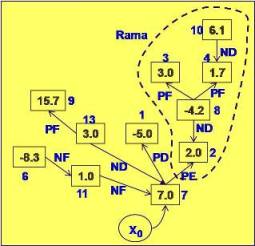
Fig. 13
- En una árbol con una raíz ficticia Xo, cada arista ek, es caracterizada por una orientación del arco ek, respecto a Xo
- Arista positiva (P), cuando el arco ek, esta orientado hacía la rama Tk (no hacía la raíz) es decir si el vértice final del arco ak es parte de la rama Tk
- Arista Negativa (N), cuando el arco está orientado hacía afuera de Tk en este caso Tk es llamado rama negativa. Ejemplo en la rama que soporte (7,13) ésta es una arista negativa y la rama que la soporta es negativa
- Arista fuerte (F), cuando la masa que soporta una arista P es positiva, o cuando la masa que soporta una arista N es negativa. Las aristas que no son fuertes se les llama débiles (D)
- Arista de aristas fuertes y positivas: (8,4), (7,2), (8,3)
- Arista positiva y débil: (7,1)
- Arista negativa y débil: (2,8), (4,10), (7,13)
- Arista negativa fuerte: (11,6), (7,11)
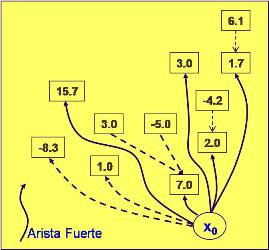
Fig. 14
- Un vértice Xk es de carácter fuerte cuando la cadena que lo une con el vértice raíz tiene alguna arista fuerte
- Arbol Normalizado: si su raíz es común a todas las aristas fuertes, cada árbol T de un grafo G puede ser normalizado, reemplazando los arcos P fuertes (Xk, Xe) por un arco que una el vértice final (de este arco fuerte) con el vértice ficticio, es decir (Xo, Xe) y el arco (Xq,Xr) de una arista N fuerte por un arco ficticio (Xo ,Xq). Iterando este procedimiento hasta que todas las aristas fuertes tenga Xo como extremidad
PRINCIPALES PASOS DEL ALGORITMO
Se construye un árbol To en el grafo G, y se entra a un proceso iterativo siguiente: La iteración (i + 1) transforma el árbol normalizado To en un nuevo árbol normalizado Ti+1. Cada árbol Ti = (X, Ai) es caracterizado por sus arcos Ai y sus vértices fuertes Yi. El Proceso termina cuando Y es un cierre de G. Cada iteración Ti+1 es realizado por los siguientes pasos (Fig. Nº 15):- Buscar un arco (Xk, Xe) en G, tal que Xk ? Yi (tal que un vértice Xk sea fuerte) y Xe ? (X- Yi) ( Xe sea débil), si existe, entonces ir al paso 2, sino ir al paso 4
- Determinar el vértice Xm la raíz de la rama fuerte que contiene a Xk . Construir el árbol Tj substituyendo el arco (Xo, Xm) de Ti con el arco (Xk, Xe). Ir al paso 3
- Normalizar el árbol Tj , con lo cual obtenemos el árbol Ti+1 , regresa al paso 1
- Se termina el proceso. Yi es el cierre máximo de G
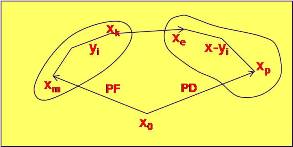
Fig. 15
El mecanismos mencionado, implica el investigar arcos, una gran cantidad de veces, que depende del número de vértices existentes yd e la situación de ellos con las consecuencias de cálculos muy pesados, difíciles de predecir en tiempo de computación.
APROXIMACIÓN DE LIPKEWICH Y BORGMAN
A partir de una publicación de Michael P. Lipkeweich y Leon Borgman, se ha podido obtener una variante de la aplicación de la teoría de grafos que simplifica el número de cálculos y obtiene resultados bien aproximados al óptimo.La simplificación consiste en tratar a los vértices (bloques económicos) nivel por nivel, trabajando primero el nivel superior (1º nivel), luego el 1º con el 2º y así sucesivamente.
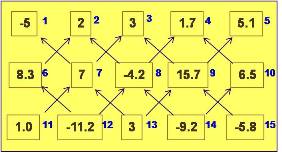 Fig. 16 |
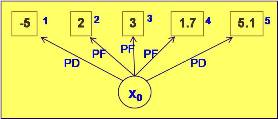 Fig. 17: PD=positivo débil, PF=positivo fuerte |
Para aplicar mas al detalle esta optimización, se expondrá un ejemplo numérico a dos dimensiones obtenido de la mencionada publicación. Partiendo de la Fig. 16 iniciamos el algorítmo con el 1º nivel.
Al normalizar el grafo únicamente con los vértices del 1º nivel, tenemos el árbol de la Fig. 17. Se extraen los bloques únicamente con vértices fuertes.
El árbol queda reducido a la Fig. 18:
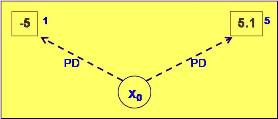 Fig. 18 |
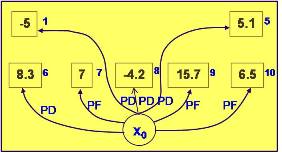 Fig. 19 |
Añadimos el 2º nivel y tenemos la Fig. Nº 19. Vemos que el vértice 7 está condicionado a la extracción de 1, pues esto lo tenemos registrado en el grafo original. Por lo tanto podemos conectar 7 a 1 con un arco, y el arco ficticio desde Xo irá a 1. Vemos en la Fig. Nº 20 que 1 será un vértice fuerte por lo tanto (Xo,1) es una arista positiva fuerte, necesariamente a extraer.
Del mismo modo, los vértices 9 y 10 están condicionados a la extracción de 5 (ver gráfico inicial). Podemos conectar el vértice 10 a 5 que formará así una masa positiva cuyo vértice 5 será fuerte, unido al Xo por una arista positiva fuerte (PF). Fig. Nº 20.
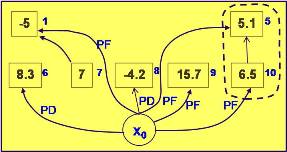 Fig. 20 |
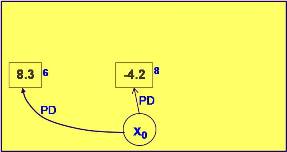 Fig. 21 |
Realizando la extracción de las masas que tienen como soporte a una arista fuerte obtenemos la Fig. 21.
A este resultado le agregamos el siguiente nivel. Fig. 22. Para poder extraer los vértices fuertes es necesario extraer los que condicionan su extrcción. Por ejemplo para extraer 11 es necesario extraer 6. Por lo tanto ambos unidos forman una masa negativa que será unido a Xo por una arista positiva débil (Fig. 23). De igual modo para extraer 13 es necesario extraer 8. Ambos forman una masa negativa que unido al vértice Xo resulta ser este arco (Xo,8) positivo débil.
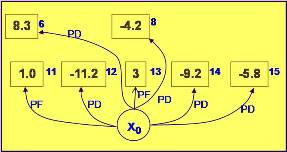 Fig. 22 |
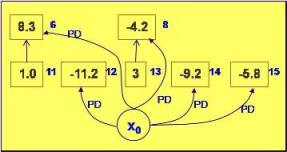 Fig. 23 |
Vemos que no podemos realizar mas extracción por no existir aristas fuertes positivas, por lo tanto el fondo del pit esta conformado por vértices negativos. Esto significa que el cierre máximo está formado por los vértices 1, 2, 3, 4, 5, 7, 9 y 10, constituyendo la solución óptima, Fig. 23.
EXTENSIÓN A TRES DIMENSIONES
Para fines de mejor claridad se presentó el procedimiento y ejemplo a dos dimensiones, en donde no se consideró la variable de la pendiente de los taludes del pit. Orientandonos a una evaluación similar a tres dimensiones, es necesario considerar las variables de gradiente de los taludes en diferentes direcciones, siendo necesario establecer una función matemática del cono (Fig. 24) que permita identificar los bloques superiores condicionantes para poder extraer los de menor nivel.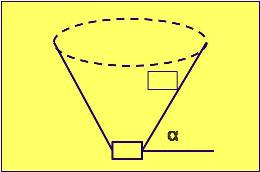
Fig. 24
Si bien la función del cono nos permite identificar los bloques superiores que condicionan la extraccion de bloques inferiores, puede ser interesante visualizar las diferentes opciones de configuracion de bloques superiores que se pueden presentar de acuerdo a la pendiente de los taludes.
Por ejemplo en la Fig. 25 se presenta dos alternativas visualizadas a tres dimensiones, analizando las gradientes que generan se presentan los ángulos según la orientación en la Fig. 26
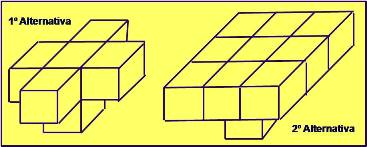
Fig. 25
En donde manteniendo una disposición de bloques uniforme y similar a la 1º alternativa, se obtienen (Fig. 26) ángulos diferentes en direcciones: 45º en la dirección A-A y 55º en la dirección B-B.
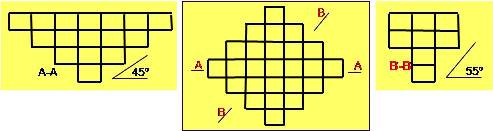
Fig. 26
De aplicarse la 2º alternativa en forma genérica, se obtendrían 45º en la dirección A-A y 35º en la dirección B-B.
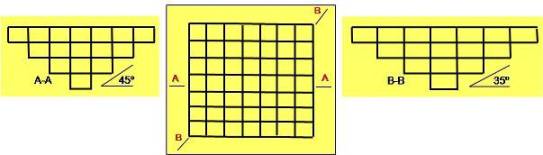
Fig. 27
Realizando la combinación de ambas alternativas, se obtiene un comportamiento simétrico en ambas direcciones (Fig. 28), siendo esta forma de disposición la que permite obtener mejor control en las gradientes. Es importante considerar que en algunos casos al aplicar métodos numéricos que nos faciliten la identificación de los bloques condicionantes, podrían también evaluarse la posibilidad de utilizar tamaños de bloques en la estimación de recursos según las gradientes deseadas en los taludes.
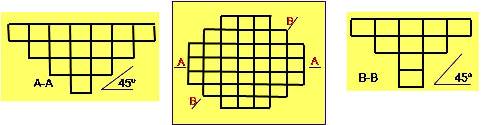
Fig. 28
En la construcción de un modelo de identificación de bloques condicionantes, la relación de extracción de un bloque con respecto a otro que se ubica encima de él, se presentaría según la Fig. 29. Por lo tanto es posible establecer los arcos de dependencia de un bloque Xk con los que condicionan su extraccción.
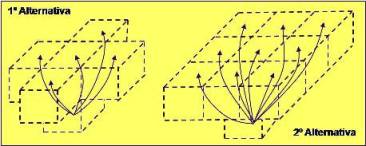
Fig. 29
Esta identificación de los bloques dependientes vienen a ser objetivamente para el caso de un Pit, la función Y= ?(x), con el conocimiento de esta función, se procede a la optimización a tres dimensiones, avanzando nivel por nivel, análogamente al caso visto a dos dimensiones.
Reciba asesoramiento para este proceso de cálculoEn Geoestadistica.com encontrará las respuestas mas convincentes para confiar en la calidad y cantidad de sus recursos. La aplicación de la mas alta tecnología mediante los software disponibles o no en su empresa, garantizaran la verificación de los resultados.Para mayor información contáctenos. |