Kriging en vetas: ejemplo de cálculo de la ley de un Tajeo
Breve Explicación Teórico / Práctica:
Si visualizamos una veta con tajeos delimitados por galerías y chimeneas como indica la figura 1, podemos extraer un tajeo y mostrarlo como indica la figura 2, en donde se observan las dimensiones del tajeo, las leyes y la potencia que se presentan en las galerías y también se presentan en las chimeneas (asumiremos que las chimeneas tienen sus leyes y potencias definidas).
 Fig. 1: Tajeos en una veta |
 Fig. 2: Un Tajeo de mineral con Leyes y Potencias |
Las variables que intervienen para la estimación de la ley del tajeo son:
- Ley (z), potencia (p) y coordenadas x de cada una de las canaletas de las galerías A1 y A2. (Fig. 3)
- Ley (z), potencia (p) y coordenadas x de cada una de las canaletas de las chimeneas A3 y A4. (Fig. 3)
- Variograma de "ley x potencia" (z * p)
- Dimensiones del tajeo (Lx en la direcció horizontal y Ly en la dirección vertical) con sus coordenadas de ubicación.
Para la estimación de la ley de cada tajeo se utilizan los valores del producto (ley x potencia), y también se debe estimar la potencia promedio por tajo, con estos dos valores se determina la ley promedio (del elemento metálico de interés).
 Fig. 3: Identificación de Variables de Cálculo |
Para los cálculos, considerar que en adición al manejo de coordenadas de las muestras, se debe tomar en cuenta que las galerías y chimeneas estarán representadas por puntos en linea, mientras el tajeo estará representado por puntos en el plano del tajeo.
Es importante destacar que la estimación puede ser realizada, en primera forma utilizando cada una de las muestras que se encuentran en las galerías y chimeneas, en segunda forma puede ser realizada utilizando las leyes y potencias promedios de las galerías.
En la primera forma en el cálculo podrían intervenir al rededor de 200 muestras, que requiere plantear y solucionar un sistema de 200 ecuaciones de krigeage, mientras en la segunda forma se requeriría solo de 5 ecuasiones de krigeage. En los casos prácticos de gran cantidad de tajeos, se podría realizar una comparación de los resultados de ambas formas de cálculo y tomar decisiones sobre la precisión obtenida en la estimación.
Para este ejemplo y por fines didácticos se mostrará el procedimiento con la segunda forma de cálculo, de esta forma se requerirá seguir los siguientes pasos:
- Calcular el variograma experimental y aplicar la modelización de éste con alguno(s) de los modelos autorizados, tales como: esférico, exponencial, lineal, gausiano, etc.
- Se deberá tomar en cuenta las anisotropías encontradas y deberán ser aplicadas al modelo del variograma.
- Cálculo de la ley media ponderada para cada galería y cada chimenea, nombraremos z1 y z2 a las leyes promedio de las galerías, z3, z4 a las leyes promedio de las chimeneas. Fig. 3.
- Nombraremos l1 y l2 a las longitudes de las galerías, l3 y l4 a las longitudes de las chimeneas.
- Se asume que las leyes promedio zi se distribuyen uniformemente en los li metros de cada galería o chimenea (i).
- Considerando el punto 3 válido, no se requerirá trabajar con el producto ley x potencia.
- Para propósitos de cálculo de los gamas promedio, se considerará al tajeo representado por puntos (Fig. 3).
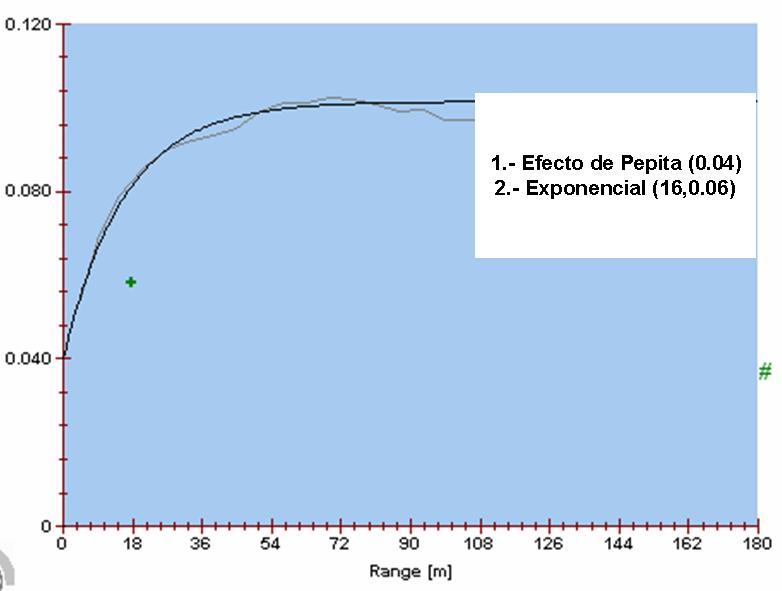 Fig. 4: Variograma Experimental y Modelo Exponencial |
En el gráfico adjunto, se muestra el variograma experimental con el modelo de variograma exponencial siguiente:

Cada punto del variogram experimental es la medida de la discrepancia promedio entre leyes distanciada a "h" metros (en el gráfico el eje horizontal Range). En cierta forma, el variograma es un indicador de como se incrementan las discrepancias entre las muestras a medida que se van distanciando entre si. ó cuando el valor de "h" crece. El modelo matemático ajustado se utilizará para el procedimiento de cálculo del krigeage.
Para explicación sobre variografía, de click aquí.
Para los cálculos, se considerará que las galerías y chimeneas estarán representadas por una línea de puntos, mientras el tajeo estará representado por puntos que representen la figura plana del tajeo.
Es muy importante destacar que la estimación puede ser realizada, en primera forma, utilizando cada una de las muestras que se encuentran en las galerías y chimeneas, y en segunda forma puede ser realizada utilizando las leyes y potencias promedios de las galerías.
La explicación de la estimación se realizará aplicando el método del krigeage ordinario, para ello debemos conocer el significado de cada una de las variables de la siguiente formulación matemática que se aplicará:
Fig. 5: Ley del tajeo (t) a estimar
Fig. 6: Sistema de Ecuaciones Krigeage
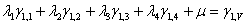
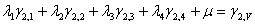
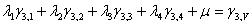
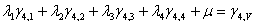
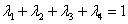
Fig. 7: Sistema de Ecuaciones de Krigeage (expandido)
En donde los símbolos
 son los pesos para cada ley zj, los
son los pesos para cada ley zj, los  ij son el promedio de aplicar el variograma entre las geometrías (i) y (j) que corresponden a cada una de las galerías, chimeneas y tajeo, como se explica a continuación:
ij son el promedio de aplicar el variograma entre las geometrías (i) y (j) que corresponden a cada una de las galerías, chimeneas y tajeo, como se explica a continuación: Con la fórmula del modelo del variograma (figura 4) y la indicación gráfica de la Fig. 6, se calcula el
 1,1 entre los puntos de la galería (1) y los mismos puntos de esta galería (1).
1,1 entre los puntos de la galería (1) y los mismos puntos de esta galería (1). Luego se calcular el
 1,2, que es el promedio del variograma entre los puntos de la galería (1) y la galería (2), de la misma forma se continúa con
1,2, que es el promedio del variograma entre los puntos de la galería (1) y la galería (2), de la misma forma se continúa con  1,3,
1,3,  1,4.
1,4. A continuación se calcula el
 1,t,
1,t,  2,t,..., hasta el
2,t,..., hasta el  4,t. También se calcula el
4,t. También se calcula el  t,t.
t,t.
 Fig. 8: Descripción Geométrica de forma de cálculo de los gama(i,j) |
Este texto es para quienes desean mayor explicación sobre el cálculo de los gama(i,j).
Como ejemplo para el cálculo del gama(2,3), se tomará un primer punto de la galería (2) y el otro extremo de "h" se ubicará en un primer punto de la chimenea (3), se calcula la distancia absoluta (por diferencia de coordenadas) y esta distancia se reemplaza en la fórmula del modelo del variograma (figura 4), se calcula el valor que da la fórmula y se registra como un primer valor.
A continuación se vuelve a tomar el primer punto de la galería (2), y en el otro extremo de "h" se ubica el segundo punto de la chimenea (3), se calcula la distancia entre estos dos nuevos puntos, esta distancia al reemplazar en la fórmula de la figura 4, originará otro valor que se debe sumar al anterior resultado. Hasta aquí tenemos 2 cálculos.
Luego se sigue la misma forma de cálculo, siempre fijando un extremo en el primer punto de la galería (2) y moviendose el otro extremo de "h" a todos los puntos de la chimenea (3). Para cada distancia "h" entre dos puntos, se seguirán acumulando los valores de gama(h) y también se seguirán contabilizando los cálculos realizados.
Una vez barrido todos los puntos de la chimenea (3), se moverá el primer extremo del vector "h" a un se gundo punto de la galería (2), el otro extremo del vector "h" barrerá de la misma forma anterior todos los puntos de la chimenea (3). Se continuará acumulando los valores de gama(h) calculados y el número de cálculos realizados.
Si la galería (2) estuviera definido por 70 puntos y la chimenea (3) estuviera definido por 50 puntos, al final de estos cálculos se habrá realizado una interacción entre los 70 puntos de la galería (2) y 50 puntos de la chimenea (3), originando (50 x 70) 3,500 cálculos de variogramas, que deben ser sumados y promediados por el número de cálculos.
Con este procedimiento obtendríamos gama(2,3), es decir el variograma promedio entre la galería (2) y la chimenea (3). El mismo procedimiento se aplica para todos los gama(i,j).
Para el cálculo de los gama(i,t), es decir gama(1,t), gama(2,t)......, gama(4,t), se considerará que el tajeo "t" esta conformado por puntos, tal como indica la figura Nº 3, la cantidad de puntos a definir al interior de "t" depende del nivel de precisión de la estimación.
Hasta aquí hemos terminado los cálculos de los gama(i,j) y gama(i,t), y tenemos definido el sistema de ecuaciones de krigeage, quedando solo las incognitas "lamda" ( ?) , que se resuelven aplicando cualquiera de los procedimientos conocidos, y si estas ecuaciones son numerosa, aplicando cualquiera de las rutinas de solución de ecuaciones lineales difundidas en la web.
La presente explicación continuará con la definición de la varianza, varianza relativa, como utilizarla y como mejorarla. Antes de terminar este punto, es importante destacar que estos procedimientos de cálculo son aplicables mediante casi todos los software especializados y que cuenten con módulos de cálculos geoestadísticos, sin embargo es necesario conocer como identificar y asignar los correctos valores geoestadisticos en los menus o pantallas que guian el proceso de estimación de recursos
Reciba asesoramiento para este proceso de cálculoEn Geoestadistica.com encontrará las respuestas mas convincentes para confiar en la calidad y cantidad de sus recursos, la aplicación de la mas alta tecnología mediante los software disponibles o no en su empresa, garantizaran la verificación de los resultados.Para mayor información contáctenos. |