DEDUCCIÓN DE LA FORMULA DE KRIGE

Para deducir la fórmula del kriging planteamos el problema siguiente: Tenemos N valores de muestras z(x1), z(x2),...., z(xN) en nuestro depósito y queremos estimar una función lineal de nuestra variable Z(x). Por ejemplo deseamos estimar los valores en un punto particular Z(xo), o el promedio en cierta región. Para poder definir y escribir todos los casos separadamente, expresamos el valor a ser estimado con:


El volumen V sería el depósito total, o el block de mineral, o podría ser un pequeño y simple punto. Podría ser incluso un volumen irregular. Para estimar Z(V) consideramos un promedio pesado de la data.


en donde son los pesos. El asterísco indicará el valor estimado para diferenciarlo del valor real desconocido en el terreno. El problema se traduce en encontrar los mejores valores para los pesos que se utilizarán en la ponderación. Es aquí en donde se aplicará el modelo geoestadístico. Consideraremos la variable regionalizada.


Los pesos a encontrar deben estar sujetos a:

1. No ocasionar sesgo en la estimación


2.- La varianza o error de estimación debe ser mínimo:

El No sesgo de los ponderadores

Asumiendo que la variable aleatoria Z(x) es estacionaria con valor promedio m. Significa que para cualquier zona se mantendrá la media m y también será la media de cualquier bloque.


La estimación de un punto se realizará asignando pesos a las muestras que se encuentran alrededor del punto a estimar, definiendose una combinación lineal siguiente:


La media del error de estimación de [Z*v - Zv] puede expresarse en términos de covarianza o variograma.


A fin de asegurar el no sesgo del interpolador, el valor esperado debe ser cero, por lo tanto m=0 o la suma de los pesos debe ser igual 1.

Varianza mínima en la estimación

La varianza del error [Z*v - Zv] se puede expresar en terminos de la covarianza y del variograma.





en donde:


es el promedio del variograma entre los puntos de las muestras y los puntos discretizados al interior del volumen V, como se indica en el siguiente gráfico.



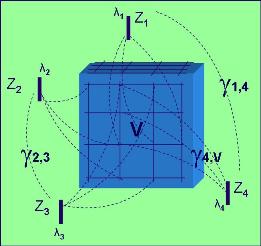es el variograma promedio entre los puntos discretizados al interior del volúmen V y si mismos, como se indica en el siguiente gráfico.


A fin de minimizar la varianza de estimación bajo condiciones que la suma de los pesos deben ser igual a 1, introducimos el multiplicador de Lagrange "u" en la expresión de la varianza a ser minimizada. Si la suma de los pesos debe ser 1.0, podemos adicionar el término "u" en la forma que se indica de tal manera que la expresión no cambia en valor.


La derivada parcial de la cantidad es por lo tanto cero, esto permite extender a N+1 las ecuaciones lineales que se denominan sistema de ecuaciones lineales para el kriging. Un poco mas abajo mostraremos los detalles de deducción matemática de esta expresión.

Cuando escribimos el sistema de ecuaciones lineales en términos del modelo del variograma resulta.



La mínima varianza de estimación denominada varianza de kriging, se expresa por:

Reciba asesoramiento para este proceso de cálculo En Geoestadistica.com encontrará las respuestas mas convincentes para confiar en la calidad y cantidad de sus recursos, la aplicación de la mas alta tecnología mediante los software disponibles o no en su empresa, garantizaran la verificación de los resultados. Para mayor información contáctenos.